Examen 3 : Préparation (Nombre complexe, algèbre et géométrie vectorielles dans l'espace)

1. Soit les vecteurs suivants :
   

   1. Calculer, si possible, .
   2. Calculer, si possible, .
   3. Calculer, si possible, .
   4. Calculer, si possible, .
   5. Calculer, si possible, .
   6. Calculer l'angle entre et .
   7. Calculer .
   8. Calculer .
   9. Construire un vecteur unitaire à et à .
   10. Démontrer que ces vecteurs forment une base de .
   11. Exprimer le vecteur .
   Réponses
   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
   7. 
   8. 
   9. et .
      On obtient donc et .

   10. Premier critère: linéairement indépendant (il faut vérifier la seule solution de est ).
       Il faut résoudre le système : .
       Ce système admet la solution mais on doit démontrer que c'est la seule solution. Or , donc la solution est unique.

       Deuxième critère: système générateur (il faut vérifier que admet au moins une solution).
       Il faut résoudre le système : .
       Ce système a les mêmes coefficients que celui du critère précédant et ainsi la même matrice des coefficients et donc une solution unique.

       
   11. On résout .
       On obtient la matrice : .

2. Vrai ou faux

   1. Le produit de deux nombres complexes n'est pas un nombre réel.
   2. Deux vecteurs non nul de l'espace sont perpendiculaires si et seulement si leur produit scalaire est nul.
   3. Il y a deux vecteurs unitaires perpendiculaires à une droite dans l'espace.
   4. Un plan dans l'espace est définit parfaitement par deux points et un vecteur.
   5. Un plan dans l'espace peut-être définit parfaitement par deux points et un vecteur.
   Réponses
   1. Faux. Par exemple, et est un nombre réel.
   2. Vrai. En effet : . Or si et alors donc et les vecteurs sont perpendiculaires.
   3. Faux. il y en a une infinité. En effet, pour une droite , tous les vecteurs parallèles au plan sont perpendiculaires à la droite .
   4. Faux. Si on a par exemple et le vecteur , il suffit que , et il n'y a pas un système générateur.
   5. Vrai. Si on a par exemple et le vecteur , il faut que

3. Soit les points , et . Trouver la valeur de pour que le triangle ABC soit rectangle en B. (5 pts)

   Réponses
   
   

4. Soit les nombres complexes suivants :

   Effectuer les opérations suivantes dans

   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
   7. 
   Réponses
   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
   7. 

5. Soit les nombres complexes suivants :

   1. Calculer .
   2. Calculer .
   3. Calculer .
   Réponses
   1. 
   2. 
   3. 

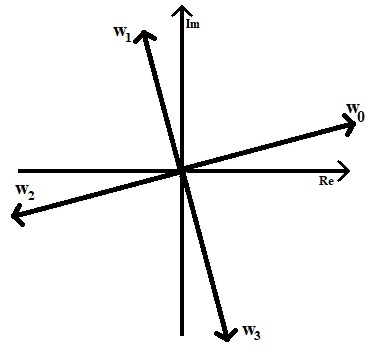
6. Trouver les 4 racines de et représenter le plan d'Argand.

   Réponses
   • 
   • 
   • 
   • 

   

7. Évaluer .

   Réponses
   

8. Trouver une équation vectorielle de la droite perpendiculaire au plan passant par le point .

   Réponses
   

9. Trouver une équation cartésienne du plan passant par le point et qui est perpendiculaire à la fois au plan et au plan .

   Réponses
   .
   
   .
   
   Et on obtient :

10. Trouver une équation cartésienne du plan qui passe pas les points , , ,

    Réponses
    Il nous faut deux vecteur du plan, disons et .
    
    . Prenons , c'est plus élégant.
    
    et on obtient :

11. Calculer le point de la droite le plus près du point et calculer la distance entre ce point et .

    Réponses
    
    
    
    
    
    
    

12. Soit les trois droites suivantes :

    • 
    • 
    • 
    Déterminer précisément la position relative de ces trois droites.
    Réponses
    • Les droite et sont parallèles distinctes. Elles sont distantes de .
    • Les droites et sont concourantes. Elles se croisent au point lorsque et .
    • Les droites et sont gauches.
      Nous avons . Et ainsi .
      Le plan construit à partir de ces droites et passant pas le point est .
      Calculons la projection avec :
      .
      Et la distance est .